Rose: Kapitel 13
| Click here for English Version | |
| Navigation: Startsteite > Othello lernen > Buch Rose | << voriges Kapitel << - >> nächstes Kapitel >> |
Kapitel 13: Zählen im Endspiel
In den Kapiteln 6 und 8 haben wir uns Strategien angesehen, die helfen können, gute Züge im Endspiel zu entdecken. In vielen Stellungen ist der einzige Weg, den richtigen Zug zu finden, jedoch eine genaue Zählung. Das heißt, Du musst in der Lage sein, eine Abfolge von Zügen für den Rest des Spiels zu berücksichtigen und herauszufinden, wie das Endergebnis des Spiels aussehen wird. Während ich Techniken erforsche, um dies so einfach wie möglich zu gestalten, erfordert es immer noch die Fähigkeit, "vorauszuschauen" und zu visualisieren, wie das Spielbrett nach den geplanten Zügen aussehen wird, was für Anfänger möglicherweise schwierig ist. Im ersten Teil dieses Kapitels wird erklärt, wie man die letzten beiden Züge des Spiels zählt, was relativ einfach ist und auch für Anfänger beherrschbar sein sollte. Der Rest des Kapitels enthält einige der schwierigsten Materialien des Buches und ist für fortgeschrittene Spieler gedacht. Unabhängig von Ihrem aktuellen Level ist das Üben des Endspielzählens eine der besten Möglichkeiten, deine Fähigkeit Vorauszuschauen zu verbessern und kann dir helfen, in allen Phasen des Spiels stärker zu werden. Der Anhang behandelt Software, die speziell zum Üben von Endspielen entwickelt wurde.
|
Diagramm 13-1 zeigt eine typische Stellung, in der das Zählen verwendet werden kann, um den besten Zug zu bestimmen. Der erste Schritt besteht darin, die Anzahl der Steine deiner eigenen Farbe auf dem Brett zu zählen. Es gibt mehrere Möglichkeiten, Steine zu zählen und die Erfahrung wird dir zeigen, welche Methode für dich am besten geeignet ist. Wenn Du ein Spiel mit Zeitlimit spielst, kommt es auf Geschwindigkeit an. Dennoch ist es wichtig, die richtige Anzahl von Steinen zu ermitteln. Daher ist es wichtig, eine Methode zu finden, mit der du genau zählen kannst. Persönlich zähle ich die Anzahl der Steine in jeder Spalte, indem ich von rechts nach links addiere. In Diagramm 13-1 gibt es zum Beispiel 7 schwarze Steine in Spalte h, plus 5 in Spalte g ergibt 12, plus 4 in Spalte f ergibt 16 usw. Mit etwas Übung wird es möglich, einfach auf die Spalte zu schauen und zu wissen wie viele Steine sie enthält, ohne wirklich zu zählen. Natürlich kannst du genausogut von links nach rechts zählen, beginnend in Spalte a und endend mit Spalte h, aber du wirst wahrscheinlich feststellen, dass es einfacher ist, entlang von Spalten als entlang von Zeilen zu addieren. Eine andere Möglichkeit zum Zählen besteht darin, die Steine in Fünfergruppen zu gruppieren, was das Hinzufügen der Gruppen erleichtert (5, 10, 15 ...). Ich habe jedoch festgestellt, dass es schwierig werden kann, sich zu merken, welche Steine bereits gezählt wurden. | |
|
Diagramm 13-1: Schwarz ist am Zug |
Nachdem wir in Diagramm 13-1 (wird unten wiederholt) festgestellt haben, dass Schwarz 26 Steine hat, zählen wir nun die Anzahl der Steine, die Schwarz am Ende des Spiels haben wird. Überlege dir, was passiert, wenn Schwarz a8 spielt (Diagramm 13-2) und Weiß dann die Partie mit b8 beendet (Diagramm 13-3). Wie viele Steine hat Schwarz? In Diagramm 13-2 hat Schwarz 26 + 7 = 33 Steine; Schwarz begann mit 26 Steinen, bekam zusätzlich fünf am linken Rand (a4, a5, a6, a7 und a8) und zwei auf der Diagonale (b7 und c6). Beim Zählen eines Zuges, der sich in zwei oder mehr Richtungen dreht, ist es oft einfacher, Steine auf diese Weise in eine Richtung nach der anderen hinzuzufügen. In Diagramm 13-3 dreht Weiß einen Stein zurück (b7) und lässt Schwarz mit 33 - 1 = 32 Steinen übrig. Wenn Schwarz also in Diagramm 13-1 a8 spielt, hat er am Ende des Spiels 32 Steine.
 |
 |

|
| Diagram 13-1: | Diagram 13-2: | Diagram 13-3: |
| Schwarz ist am Zug | Weiß ist am Zug | Schwarz hat 32 Steine |
Es ist zwar möglich, auf diese Weise zu zählen, indem man zuerst berechnet, dass Schwarz in Diagramm 13-2 33 Steine hat und dann am Ende des Spiels 32 Steine bleiben, was ich die Zwei-Stufen-Methode nennen würde. Du kannst dir aber einen Schritt sparen, indem du den Punktestand von Diagramm 13-3 direkt ermittelst. Immerhin, wenn wir in Diagramm 13-1 an den Zug nach a8 denken, wissen wir, dass Schwarz am Ende der Partie den Stein auf b7 nicht behalten wird, weil Weiß nach b8 ziehen wird. Anstatt also Schwarz diesen Stein zuzurechnen, nur um ihn dann wieder abzuziehen, ist es einfacher ihn gar nicht erst zu zählen.
Wenn ich diese Stellung zählen würde, würde ich mit 26 beginnen, fünf für die Steine am linken Rand hinzufügen um 31 zu bekommen und dann eins für den Stein auf c6 hinzufügen, um 32 zu erhalten. Wenn du es noch nie zuvor gemacht hast, könnte es so aussehen als ob diese „Abkürzung“, in einem Schritt direkt zu Diagramm 13-3 zu gehen, das Zählen schwieriger und fehleranfälliger macht. Nachdem ich jedoch Jahre mit beiden Methoden verbracht habe, versichere ich dir, dass du durch das Weglassen des zusätzlichen Schrittes schneller und mit weniger Fehlern zählen kannst. Der Unterschied zwischen diesen beiden Methoden sollte deutlicher werden, wenn wir uns ansehen, was passiert, wenn Schwarz in Diagramm 13-1 mit b8 beginnt.
Beginnend mit Diagramm 13-1, wenn Schwarz mit b8 beginnt, wird das Ergebnis in Diagramm 13-4 gezeigt. Weiß beendet die Partie mit a8 (Diagramm 13-5). Wie viele Steine hat Schwarz? In Diagramm 13-4 hat Schwarz 26 + 14 = 40 Steine; Schwarz begann mit 26 Steinen, bekam zusätzlich fünf am unteren Rand (b8, c8, d8, e8 und f8), fünf auf der Diagonale (c7, d6, e5, f4 und g3) und vier auf Spalte b (b4 , b5, b6 und b7); beachte, dass b8 bereits oben enthalten war). In Diagramm 13-5 dreht Weiß sieben Steine zurück (b7, b8, c8, d8, e8, f8 und g8) und lässt Schwarz 40 - 7 = 33 Steine. Wenn Schwarz also b8 in Diagramm 13-1 spielt, hat er am Ende der Partie 33 Steine. Da a8 für Schwarz 32 Steine und b8 Schwarz für 33 Steine ergibt, ist b8 der bessere Zug.
 |

|
| Diagramm 13-4: | Diagramm 13-5: |
| Weiß ist am Zug | Schwarz hat 33 Steine |
Verwendest du die einstufige Methode, um die Anzahl der Steine in Diagramm 13-5 zu berechnen, beginnst du wieder mit 26, der Zählung in Diagramm 13-1. Schwarz gewinnt dann fünf Steine auf der Diagonale (c7, d6, e5, f4 und g3) ist 31 und drei Steine auf Spalte b (b4, b5 und b6), um 34 zu bilden. Schließlich, wenn Weiß nach a8 zieht, verliert Schwarz den Stein auf g8 (beachte, dass wir die anderen Steine am unteren Rand nie zur Summe von Schwarz addiert haben, also müssen sie jetzt nicht abgezogen werden), und am Ende der Partie hat Schwarz 34 - 1 = 33 Steine. Ich persönlich finde es viel einfacher, auf diese Weise zu zählen, als 26 + 14 = 40 nach b8 und 40 - 7 = 33 nach Weiß a8 zu berechnen.
An dieser Stelle sollte ich noch eine andere Zählmethode erwähnen, die ich Plus/Minus-Methode nenne. Oben haben wir die Anzahl der Steine am Ende der Partie für a8 und b8 verglichen, um festzustellen, dass b8 besser war. Eine andere Möglichkeit, einen Zug auszuwählen, besteht darin, stattdessen die Anzahl der gewonnenen oder verlorenen Steine zu berechnen. Wenn wir Diagramm 13-1 und Diagramm 13-3 vergleichen sehen wir, dass Schwarz am Ende der Partie 6 Steine gewinnt, indem es a8 spielt (a4, a5, a6, a7, a8 und c6). Ein Vergleich von Diagramm 13-1 und Diagramm 13-5 zeigt, dass Schwarz 7 Steine gewinnt, wenn es b8 spielt (8 neue Steine auf c7, d6, e5, f4, g3, b4, b5 und b6 abzüglich eines Steins auf g8). Da der Gewinn für b8 (+7) größer ist als für a8 (+6), wissen wir, dass b8 der bessere Zug ist.
Der Hauptvorteil der Plus/Minus-Methode besteht darin, dass die Anzahl der schwarzen Steine in Diagramm 13-1 nicht gezählt werden muss. Wenn a8 +6 und b8 +7 ist, dann ist b8 besser, Ende der Geschichte. Wenn mir jemand 5 Sekunden gibt, um den richtigen Zug zu finden, könnte ich das mit der Plus-/Minus-Methode machen, aber ich brauche vielleicht 10 Sekunden, um zu zählen, dass es in Diagramm 13-1 26 schwarze Steine gibt. Wenn du dir darüber hinaus die Mühe machst, die Anzahl der Steine in der Anfangsposition zu zählen, kannst du mit der Plus-/Minus-Methode immer noch denEndstand bestimmen. Wenn wir in unserem Beispiel berechnen, dass b8 +7 ist, muss die endgültige Steineanzahl die Anfangszahl 26 plus 7 oder 33 sein.
Wenn du nie planst, Positionen mit mehr als 2 leeren Feldern zu zählen, dann ist Plus/Minus wahrscheinlich besser als das Zählen aller Steine. Die Hauptvorteile des Zählens aller Steinen werden erst sichtbar, wenn du anfängst, längere Zugfolgen zu zählen. Der Grund für das Zählen besteht oft nicht darin, den besten Zug zu bestimmen, sondern einen Zug zu finden, der gut genug ist, um zu gewinnen. Wenn du Steine zählst und eine Zugfolge findest, bei der du 33 Steine erreichst, weißt du, dass du gewinnen kannst. Wenn du eine Zugfolge von +10 findest, reicht das, um zu gewinnen? Die einzige Möglichkeit dies zu wissen besteht darin, die Anzahl der Steine in der ursprünglichen Stellung zu zählen, was den Hauptvorteil der Plus-/Minus-Methode aufhebt. Tatsächlich habe ich, wenn ich mit Plus/Minus zähle, normalerweise einen „Zielwert“, der mir sagt, ob ich genug habe, um zu gewinnen. In unserem Beispiel, beginnend mit 26 Steinen, wäre das Ziel +7; das heißt, wenn ich einen Zug mit +7 oder besser finde, weiß ich, dass ich gewinnen kann. Bei einer langen Endspielzählung, bei der viele mögliche Zugfolgen berücksichtigt werden, kann es jedoch schwierig sein, das Ziel im Auge zu behalten. Beim Zählen der Steine ist immer klar, dass 33 Steine gewinnen.
Ein weiterer Nachteil der Plus-/Minus-Methode besteht darin, dass sie verwirrend sein kann, wenn du Steine in der betrachteten Reihenfolge verlierst. Angenommen, du beginnst mit 45 Steinen, verlierst aber im weiteren Verlauf des Spiels Steine. Es ist offensichtlich, dass das Ergebnis mit 33 Steinen besser ist als mit 32, aber ist -12 besser als -13? Das mentale Zählen „45 - 5 = 40, - 5 = 35, + 2 = 37, - 4 = 33“ ist einfacher als „-5 - 5 = -10, + 2 = -8, - 4 = -12“.
Da du entweder den einstufigen oder den zweistufigen Ansatz verwenden und entweder Steine zählen oder Plus/Minus verwenden kannst, gibt es wirklich vier verschiedene Möglichkeiten zu zählen. Obwohl ich dringend empfehle, einstufig statt zweistufig zu zählen, ist es wirklich eine Frage der persönlichen Vorliebe, ob du Steine zählen oder Plus/Minus verwendest; du kannst sicherlich mit beiden Methoden effektiv sein. Als ich damals anfing, Othello zu spielen, als noch Dinosaurier die Erde durchstreiften, zählte soweit ich weiß jeder nach der zweistufigen Plus-/Minus-Methode, und auch heute noch zählen einige Experten so. Um 1990 wechselte ich zu One-Step Plus/Minus und erst im Jahr 2000 begann ich endlich mit dem Zählen von Steinen. Da ich viel Erfahrung mit beiden Methoden habe, würde ich empfehlen, bei längeren Zugfolgen Steine über Plus/Minus zu zählen.
Aufhebung
Unabhängig davon, welche Methode du zum Zählen verwendest, kann eine Technik, die ich Aufhebung nenne, das Zählen erleichtern. Ziehe in Erwägung, die Position in Abbildung 13-6 mit der Plus-/Minus-Methode auszuzählen. Um die Zugfolge Schwarz a8, Weiß b8 zu zählen, würden wir normalerweise sagen, dass Schwarz zwei Steine (a7 und a8) für +2 gewinnt und zwei Steine (b5 und b6) für 0 verliert. durch Aufhebung verrechnen wir die gewonnenen Steine (a7 und a8) mit den verlorenen Steinen (c5 und c6) und erhalten sofort das Ergebnis 0 (siehe Diagramm 13-7). Um die Abfolge Schwarz b8, Weiß a8 auszuzählen, heben sich die vier gewonnenen Steine (c7, d6, e5 und f4) durch vier verlorene Steine (c6, d5, e4 und f3) auf, so dass ein zusätzlicher Stein auf g3 übrigbleibt. Somit ist diese Folge +1 für Schwarz (siehe Diagramm 13-8).
 |
 |

|
| Diagram 13-6: | Diagram 13-7: | Diagram 13-8: |
| Schwarz ist am Zug | Schwarz a8, Weiß b8 | Schwarz b8 Weiß a8 |
|
Die Aufhebung ist am nützlichsten in Situationen wie Diagramm 13-8, in denen die sich aufhebenden Steine auf benachbarten Feldern oder zumindest nahe beieinander liegen. Wenn sich die Steine auf gegenüberliegenden Seiten des Bretts befinden, finde ich es üblicherweise besser, einfach zu zählen, ohne die Aufhebung anzuwenden. Wenn du deine Augen immer wieder von einem Teil des Bretts zum anderen verschieben musst, um die sich aufhebenden Steine in einer Reihe zu platzieren, wird es wahrscheinlicher, dass du einen Fehler machst. Eine Ausnahme davon ist, wenn sich eine große Anzahl von Kantensteinen gegeneinander aufheben, wie z. B. Diagramm 13-9. Betrachtet man die Folge Schwarz a8, Weiß b8 kann es sich lohnen, fünf Kantensteine miteinander zu verrechnen, was das Ergebnis von +1 ergibt. Wie ich in diesem Kapitel bereits erwähnt habe, kannst du durch Übung und Erfahrung herausfinden, ob dir diese Technik das Zählen erleichtert. | |
|
Diagramm 13-9: Schwarz ist am Zug |
Verzweigung
In den obigen Beispielen mit nur zwei leeren Feldern wird das Endergebnis der Partie bestimmt, sobald Schwarz einen Zug wählt, da Weiß einfach das letzte leere Feld ausfüllt, um das Spiel zu beenden. Sobald du beginnst, Positionen mit mehr leeren Feldern zu zählen, hat dein Gegner möglicherweise mehr als einen Zug zur Auswahl. Dann ist es notwendig, nicht nur darüber nachzudenken, welchen Zug du spielen möchtest, sondern auch darüber, welchen Zug dein Gegner als Reaktion wählen wird. Selbst bei nur drei leeren Feldern kann dies das Herausfinden des besten Zugs erheblich erschweren. Betrachte zu diesem Beispiel Diagramm 13-10.
 |
|
| Diagram 13-10: | Diagram 13-11: |
| Weiß ist am Zug | Mögliche Zugfolgen aus Abbildung 13-10 |
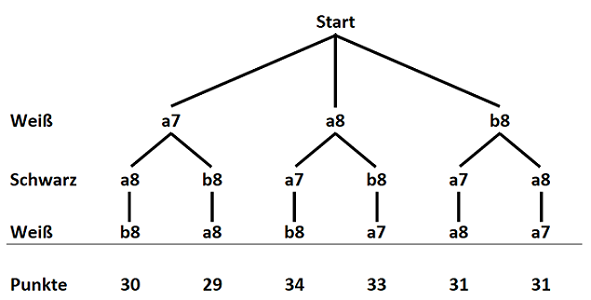
Weiß kann zwischen einem der drei leeren Felder wählen, und nach seinem Zug kann Schwarz auf eines der beiden verbleibenden Felder spielen. Dies bedeutet, dass 3 x 2 = 6 mögliche Abfolgen zu berücksichtigen sind. Diese sind in Diagramm 13-11 zusammen mit dem Ergebnis für Weiß nach jeder Zugfolge gezeigt (z. B. nach der Zugfolge Weiß a7, Schwarz a8, Weiß b8 hat Weiß am Ende der Partie 30 Steine). Was sind angesichts dieser Informationen die besten Züge für beide Seiten?
Wenn Weiß mit a7 beginnt, wählt Schwarz zwischen a8 und b8. Wenn Schwarz a8 spielt, hat Weiß am Ende 30 Steine, was bedeutet, dass Schwarz 34 hat. Wenn Schwarz b8 spielt, dann hat Weiß am Ende 29 Steine und Schwarz hat 35. Schwarz wird natürlich den Zug wählen, der ihm die meisten Steine und Weiß so wenig Steine wie möglich lässt. Wenn Weiß also mit a7 beginnt, folgt Schwarz mit b8 und Weiß hat am Ende der Partie 29 Steine. Wenn Weiß mit a8 beginnt, wählt Schwarz b8 und Weiß erhält 33 Steine. Wenn Weiß mit b8 beginnt, ergeben beide Antworten von Schwarz die gleiche Anzahl und Weiß bleiben 31 Steine. Da Weiß mit a8 beginnend 33 erzielen kann, aber nur 31 mit b8 und 29 mit a7, muss der beste Zug von Weiß in Diagramm 13-10 a8 sein, und Schwarz antwortet mit b8.
Das obige Beispiel zeigt, wie kompliziert das Zählen des Endspiels erscheinen kann, wenn der Gegner verschiedene Züge zur Auswahl hat. Die gute Nachricht ist, dass wir den Prozess in der Praxis erheblich vereinfachen können und es wirklich nicht so schwer ist, den richtigen Zug in Abbildung 13-10 zu finden. Angenommen, du spielst Weiß ohne die Informationen von Diagramm 13-11. Der erste Schritt beim Zählen dieser Position besteht darin, die aktuelle Anzahl von Steinen für Weiß zu zählen, die 24 beträgt. Als nächstes musst du entscheiden, welche der drei Möglichkeiten du zuerst in Betracht ziehst. Normalerweise ist der erste zu berücksichtigende Zug der, der ohne zu zählen instinktiv am besten aussieht. Angenommen, du möchtest mit b8 beginnen. Diagramm 13-12 zeigt die resultierende Stellung, und Weiß hat jetzt 30 Steine (in einer echten Partie müsste man das natürlich vor seinem geistigen Auge haben).
 |
 |

|
| Diagram 13-12: | Diagram 13-13: | Diagram 13-14: |
| Weiß hat 30 Steine | Weiß hat 31 Steine | Weiß hat 29 Steine |
Wenn wir der Logik von Diagramm 13-11 folgen, müssen wir jetzt das Endergebnis jeder schwarzen Wahlmöglichkeit zählen, um zu bestimmen, was (für Schwarz) am besten ist; erst dann wissen wir, wie viele Steine Weiß am Ende der Partie haben wird, wenn Weiß mit b8 beginnt. In der Praxis ist es am besten, das Endergebnis zu zählen, wenn Schwarz auf a8 spielt (und Weiß mit a7 abschließt), da dies wesentlich einfacher ist, als die Zugfolge a7-a8 zu zählen. Nach Schwarz a8, Weiß a7 ist die einzige Änderung für Weiß der zusätzliche Stein auf a7 (siehe Diagramm 13-13). Da Weiß in Diagramm 13-12 30 Steine hat, muss er in Diagramm 13-13 31 Steine haben. Um sicher zu gehen, dass Weiß mit b8 in Diagramm 13-10 wirklich 31 Steine bekommen kann, müssen wir die Reihenfolge auszählen, wenn Schwarz in Diagramm 13-12 a7 wählt. Vielleicht ist a7 besser für Schwarz und Weiß bekommt weniger als 31 Steinen. Aber auch ohne diese Abfolge zu zählen, ist klar: Weiß verliert, wenn er mit b8 beginnt. Die einzige Frage ist, wie hoch er verlieren wird. Anstatt Zeit damit zu verbringen das herauszufinden, ist es sinnvoller, eine der anderen Möglichkeiten in Abbildung 13-10 auszuprobieren. Angenommen, du entscheidest dich als nächstes a8 zu versuchen, was zu der in Diagramm 13-14 gezeigten Stellung führt, in der Weiß 29 Steine hat.
Auch hier müssen wir entscheiden, welchen Zug von Schwarz wir zuerst zählen. In diesem Fall scheint b8 die naheliegende Wahl zu sein, da zwei Steine am unteren Rand bleiben. Weiß schließt mit a7 ab und die Endstellung ist in Diagramm 13-15 dargestellt. Vergleicht man dies mit Diagramm 13-14, erhält Weiß vier Steine (a7, b6, c5 und c7), sodass insgesamt 33 Steine übrigbleiben. Es scheint also, dass Weiß gewinnen kann, wenn er in Diagramm 13-10 mit a8 beginnt. Wir müssen uns jedoch sicher sein, dass in Diagramm 13-14 b8 wirklich der beste Zug für Schwarz ist. Wenn Schwarz stattdessen a7 spielt, endet Weiß mit b8 (Diagramm 13-16). Vergleicht man die Diagramme 8-14 und 8-16, hat Weiß fünf Steine (b5, b6, b8, c7 und c8) mehr, insgesamt 34. Wenn Weiß also mit a8 beginnt, kann Schwarz nichts Besseres tun, als mit b8 zu antworten. und Weiß gewinnt 33-31.
 |
 |
|
| Diagram 13-15: | Diagram 13-16: | Diagram 13-17: |
| Weiß hat 33 Steine | Weiß hat 34 Steine | Weiß hat 29 Steine |
Nachdem du nun festgestellt hast, dass Weiß a8 gewinnt, möchtest du vielleicht aufhören zu zählen und einfach a8 spielen. Nehmen wir jedoch an, du möchtest sicherstellen, dass a8 wirklich der beste Zug ist. Dann musst du die endgültige Wahl von Weiß in Diagramm 13-10 berücksichtigen, nämlich a7 (Diagramm 13-17). Bei nur 29 Steinen in Diagramm 13-17 ist sofort klar, dass Weiß nicht mehr als 33 Steine bekommen wird (das Ergebnis, wenn Weiß mit a8 beginnt), und Weiß kann a7 zugunsten von a8 ablehnen.
Wie die obige Analyse zeigt, ist es zum Finden des besten Zugs nicht notwendig, die Punktzahl für jede mögliche Zugfolge zu ermitteln. In diesem Beispiel haben wir 4 von 6 Zugfolgen betrachtet. In einigen Fällen ist es sogar möglich, den richtigen Zug zu finden, indem man nur einen kleinen Prozentsatz der Zugfolgen betrachtet. Dies gilt insbesondere dann, wenn wir bereit sind, jeden gewinnenden Zug zu akzeptieren, anstatt den absolut besten Zug zu finden. Dennoch machen Verzweigungen das Zählen sicherlich komplizierter, weshalb erfahrene Spieler normalerweise nach Gewinnfolgen ohne Verzweigungen suchen. Einige Beispiele hierfür finden Sie im nächsten Abschnitt.
Zählen mit mehr als zwei leeren Felder
In diesem Abschnitt werden Techniken zum Zählen von Positionen mit mehr als zwei leeren Feldern beschrieben. Wie im ersten Teil dieses Kapitels erwähnt, gibt es mehrere Möglichkeiten, mit nur zwei Leerfeldern zu zählen, und natürlich sind beim Zählen längerer Zugfolgen noch mehr Variationen möglich. Im Folgenden gehe ich einige Beispiele dafür durch, wie ich eine Position zähle, aber ich würde nie behaupten, dass dies der einzig richtige Weg ist. Durch Übung und Erfahrung kannst du herausfinden, welche Methoden für dich am besten geeignet sind.
Wie im vorherigen Abschnitt über Verzweigungen gezeigt, müssen wir beim Zählen mit mehr als zwei leeren Feldern nicht nur Zugfolgen auszählen, sondern auch überlegen, welche Zugfolgen wir zählen sollen. In Diagramm 13-18 hat Schwarz drei Möglichkeiten, nach denen Weiß jeweils auch drei Möglichkeiten hat, und nach einigen dieser Zugfolgen hat Schwarz zwei Züge zur Auswahl. Glücklicherweise müssen wir uns nicht die Mühe machen, all diese Möglichkeiten auszuzählen. Der Schlüssel zum Zählen dieser Position ist die Verwendung der Theorie der Parität (siehe Kapitel 8), um zu entscheiden, welche Zugfolgen gezählt werden sollen.
 |
 |

|
| Diagram 13-18: | Diagram 13-19: | Diagram 13-20: |
| Schwarz ist am Zug | nach h2, a1 | nach h2 |
Egal wo Schwarz in Diagramm 13-18 spielt, die obere rechte Region hat noch zwei Felder übrig, während die obere linke Region ein Feld (a1) hat. Die Theorie der geraden Zahlen sagt uns, dass Weiß wahrscheinlich in seinem Zug a1 spielen möchte, so dass Schwarz das Spiel in das letzte Paar einleiten kann. Wenn Schwarz mit h2 beginnt, dann erzeugt dies eine Hyperregion (Region mit gerader Anzahl Leerfelder, in die Schwarz nicht spielen kann), sodass Weiß selbst dann, wenn Weiß mit a1 fortfährt, das Spiel in die Region einleiten muss. Daher beginnt diese Zählung mit einem schwarzen Zug nach h2 und der weißen Antwort auf a1. Die resultierende Position ist in Abbildung 13-19 dargestellt. Die Frage ist nun, wo will Weiß spielen, g1 oder h1?
Es gibt mindestens zwei Möglichkeiten, mit dieser Situation umzugehen. Eine besteht darin, die Steine in Diagramm 13-19 zu zählen und diese dann als Startposition zu verwenden, um beide Zugfolgen zu zählen (Weiß g1, Schwarz h1 und Weiß h1, Schwarz g1). Mit dieser Methode müssen wir die Anzahl der schwarzen Steine in Diagramm 13-19 bestimmen. Um dies zu tun, zählen wir zuerst die Anzahl der Steine in Diagramm 13-18, die 23 beträgt. Der Zug von Schwarz nach h2 gibt Schwarz sechs Steine am rechten Rand (h2, h3, h4, h5, h6 und h7) = 29, + g3 = 30 und fünf Steine in der zweiten Reihe (c2, d2, e2, f2 und g2) ergeben 35. Der Zug von Weiß nach a1 dreht den Stein auf b2 um. Somit bleiben Schwarz in Diagramm 13-19 34 Steine. Jetzt, da wir diese Zahl kennen, können wir für beide Entscheidungen von Weiß bis zum Ende der Partie zählen. Erstens, wenn Weiß g1 spielt und Schwarz h1 spielt, dann verliert Schwarz Steine auf f2 und g3 ergibt 32 und gewinnt den Stein auf h1 für 33. Wenn stattdessen Weiß h1 spielt und Schwarz g1 spielt, dann verliert Schwarz den Stein auf f3 ergibt 33 und erhält den Stein auf g1 ergibt 34. Somit kann Weiß in Diagramm 13-19 nicht besser als g1 abschneiden und Schwarz gewinnt 33-31.
Eine andere Möglichkeit, sich der gleichen Anzahl zu nähern, besteht darin herauszufinden, welcher Zug in Diagramm 13-19 für Weiß besser ist, bevor Sie das Endergebnis der Partie berechnen. In diesem Fall würden wir die Plus-/Minus-Methode verwenden und aus der Sicht von Weiß zählen. Wieder ausgehend von Diagramm 13-19 erhält Weiß nach Weiß g1 und Schwarz h1 drei Steine (g1, f2 und g3). Wenn Weiß stattdessen h1 spielt, erhält Weiß nach Schwarz g1 zwei Steine (h1 und f3). Daher nehmen wir in Diagramm 13-19 an, dass Weiß g1 spielen wird. Dann können wir beginnend mit Diagramm 13-18 (irgendwann müssen wir zählen, dass 23 schwarze Steine in dieser Stellung liegen) die gesamte Zugfolge Schwarz h2, Weiß a1, Aussetzen, Weiß g1, Schwarz h1 zählen. Zuerst würde ich bemerken, dass Schwarz am Ende der Partie die gesamte rechte Kante besitzt und sieben Steine (h1, h2, h3, h4, h5, h6 und h7) erhält, also insgesamt 30. Schwarz bekommt auch g2 = 31, drei weitere Steine in Reihe 2 (c2, d2, e2) = 34, verliert aber b2 = 33.
Im Allgemeinen würde ich die Erstere der beiden Methoden bevorzugen, weil sie einfacher ist, obwohl die letztere etwas schneller sein könnte, da wir direkter zur Endstellung gehen (bei Ersterer zählen wir f2 und g3 für Schwarz und ziehen sie später ab). Die Praxis wird dir zeigen, welche Methode für dich am besten geeignet ist, aber ich glaube, wenn die Anzahl der leeren Felder größer ist, wird es sehr schwierig, die bei der letztgenannten Methode erforderliche Visualisierung zu handhaben. Wenn du bis zu einer Zwischenposition zählst, wie z. B. Diagramm 13-19, wird dir manchmal sofort klar, dass du entweder gewinnen oder verlieren wirst. In unserem Beispiel liegen die Spielstände nahe beieinander, also müssen wir in Diagramm 13-19 an beide Züge von Weiß denken. Wenn Schwarz jedoch zu diesem Zeitpunkt 38 Steine hätte, würden wir ohne weitere Zählung wissen, dass Schwarz gewinnen wird, oder wenn Schwarz 26 Steine hätte, würden wir wissen, dass Schwarz verlieren wird.
Nachdem wir berechnet haben, dass Schwarz nach Schwarz h2, Weiß a1 gewinnt, ist es einfach zu schließen, dass nach h2 (Diagramm 13-20) Schwarz gewinnt, egal wohin Weiß zieht. In diesem Fall sind der obere rechte Bereich (g1 und h1) und der obere linke Bereich (a1) unabhängig. Das heißt, egal ob Weiß zuerst die rechte obere Region oder zuerst a1 spielt, die umgedrehten Steine sind identisch. Wenn Weiß also g1 statt a1 spielt, hat Schwarz immer noch 33 Steine.
Wenn wir in Diagramm 13-18 überprüfen wollen, dass h2 der beste Zug von Schwarz ist, müssen wir die anderen schwarzen Optionen, nämlich g1 und h1 in Betracht ziehen. Wie bereits erwähnt, sagt uns die Theorie der geraden Zahlen, dass in beiden Fällen die erste zu berechnende Folge eine Antwort von Weiß a1 ist. Nach Schwarz h1, Weiß a1, ist Schwarz h2 offensichtlich die beste Wahl. Nach Schwarz g1, Weiß a1 werden die letzten beiden Züge (Schwarz h2, Weiß h1) erzwungen. Wir brauchen also nur zwei Folgen zu zählen, nämlich h1, a1, h2, g1 und g1, a1, h2, a1. Diese werden als Übung belassen, aber es ist nicht schwer zu überprüfen, dass keine dieser Zugfolgen zu den 33 Steinen passt, die Schwarz bekommen kann, wenn man mit h2 beginnt. Am Ende war es nur notwendig, vier Zugfolgen auszuzählen, um zu überprüfen, ob h2 der beste Zug in Diagramm 13-18 ist.
Diagramm 13-21 zeigt eine Position aus einem meiner Spiele bei der WM 2001. Den besten Zug in der Position zu finden und zu überprüfen ist nicht einfach; WZebra gab die Position an und betrachtete 3.440 Zugfolgen, bevor es h1 wählte. In der eigentlichen Partie habe ich diesen Zug nicht gefunden, aber ich habe eine Gewinnfolge gespielt, die recht einfach zu zählen war. Zuerst habe ich gezählt, dass Weiß 19 Steine hat. Mit Blick auf die Stellung dachte ich, dass a3 ein guter Zug wäre, da er vier innere Steine (b4, c5, d6 und e7) umdreht; Schwarz hat nur einen Zug, a2, was Weiß 23 Steine übriglässt.
 |
 |

|
| Diagram 13-21: | Diagram 13-22: | Diagram 13-23: |
| Weiß ist am Zug | Weiß ist am Zug | letzte Züge |
Jetzt ist die obere linke Region immer noch eine Hyperregion für Schwarz, und eine Möglichkeit mit dieser Region umzugehen, besteht darin, schwarze Züge in diese Region zu füttern (siehe Kapitel 8). Ich beschloss, b1 zu betrachten, was Schwarz zwei Möglichkeiten gibt, b2 und c1. Allerdings ist b2 schrecklich, so dass Weiß h1, Aussetzen, c1, Aussetzen, a1 spielen kann. Also muss Schwarz nach c1 ziehen. Diese beiden Züge geben Weiß zusätzliche Steine auf b1 und d3, aber Schwarz wird schließlich auf a1 ziehen und den Stein auf b1 umdrehen. Daher habe ich nur den Stein auf d3 hinzugefügt, wodurch 24 weiße Steine entstanden sind (Diagramm 13-22). Die restlichen Züge, die in Diagramm 13-23 gezeigt werden, sind offensichtlich und lassen Schwarz keine Wahl. Es ist auch ziemlich einfach, diese Zugfolge zu zählen. Weiß gewinnt fünf Steine oben links (b2, c2, d2, b3 und c3) ergibt 29 und vier Steine oben rechts (f1, g1, h1 und h2) ergibt 33. In diesem Fall brauchte ich wirklich nur eine Zugfolge zu zählen, um einen Gewinnzug zu finden.
Übungen
Finden Sie in jedem Diagramm den besten Zug und bestimmen Sie das Endergebnis des Spiels mit perfektem Spiel von beiden Seiten. Antworten findest du hier.
 |
 |

|
| Übung 13-1: | Übung 13-2: | Übung 13-3: |
| Schwarz ist am Zug | Schwarz ist am Zug | Schwarz ist am Zug |
 |
 |

|
| Übung 13-4: | Übung 13-5: | Übung 13-6: |
| Weiß ist am Zug | Weiß ist am Zug | Weiß ist am Zug |
| Navigation: Startsteite > Othello lernen > Buch Rose | Günther Beyer 19:54, 24. Jan. 2022 (CET) | << voriges Kapitel << - >> nächstes Kapitel >> |
