Rose: Chapter 11

Klicke hier für Deutsche Version
Navigation: Main Page > Learn Othello > Book Rose	‎<< previous chapter << - >> next chapter >>

---

Chapter 11: Book openings

This chapter examines book openings, i.e., moves that are prepared and memorized before the game begins; an opening book is a collection of openings. As noted in Chapter 4, novice players really do not have to worry that much about openings. However, having well prepared book openings becomes vital as you come up against stronger players. Rather than a long list of moves to be studied, this chapter is meant to teach you how to go about developing openings of your own.

If you have played even a few dozen games of Othello, you have probably noticed the same patterns being repeated in the first moves of the game. If you remember what you did the last time you saw a certain position, you might make the same move without really thinking about it. Or, perhaps the move you used last time did not work out well, and you started to look for some alternative. While simply playing games will eventually give you a feel for which moves are good and which are bad, developing an opening book with the aid of computer analysis can make this process much easier and more effective.

Example of developing an opening

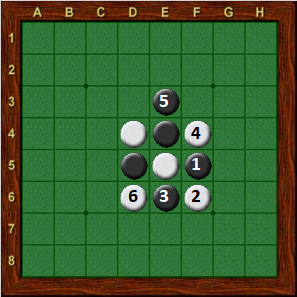
Suppose that you are black and played the opening shown in Diagram 11-1. Your opponent chose to play the “chimney” opening (6. d6), resulting in Diagram 11-2, at which point you had no idea what to play next. You want to build up your opening book so that the next time this position occurs, you will be prepared with a good response. The easiest thing to do would be to have a computer suggest a move; suppose the computer recommends 7. g4, as shown in Diagram 11-3.

Diagram 11-1	Diagram 11-2	Diagram 11-3
Chimney	Black to move	White to move

You might choose to stop at this point, and simply add Diagram 11-3 to your opening book. The next time someone plays the chimney, you can play g4 without having to think about it. That is all well and good, but you should be at least a little bit curious about what White will do in response to your g4 move. In Diagram 11-3, White has seven moves to choose from; searching the Thor database (see Appendix for details) reveals that all of these moves have been played at least once. Ideally, we would like to know what to do against each of White’s possible responses. We could try each move for White, then ask the computer for a suggested reply as Black. Our book would then look like:

		8. d3	Our move
6. d6	Our move	8. e2	Our move
		8. f2	Our move
(Four other move 8’s not shown)

Of course, once you have come this far, you may start to wonder about what White will do after your move 9. For example, if White plays 8. d3 and you make your prepared move 9. c3, this leaves White with quite a few reasonable looking options for move 10. Looking the position up in the database shows that 7 different moves have been used at move 10. You could again ask the computer to find a good move against each of these 7 moves. The problem though is that if you put in every possible response to each of your moves, the size of your opening book will grow exponentially. If your opponent always has 7 possible moves to choose from then the number of lines that you would have to remember will grow to 7x7 = 49, then 7x7x7= 343, then 7x7x7x7= 2401 and so on. To put that in perspective, when I won the World Championship my entire opening book with both colors had around 300 lines. Even for a computer program, which might have a million lines in its opening book, it is impossible to include everything.

Thus, it is important to be very selective when choosing what to put into your opening book. To help in the selection process, I actually keep two separate books. One book has all of the research that I have conducted, and contains a lot more openings than I actually know. The other book contains “cheat sheets” for the particular openings that I intend to use and want to have memorized. The cheat sheets are color specific— if there is a certain opening that I might play with either color, it will appear once in the section with black openings and again in the section with white openings. When I am building a new opening, I will put all of the research into the large book. Once the research is finished, I decide which lines to put onto the cheat sheets, and then try to memorize those lines.

Of course, you still must figure out what openings to research in the first place. For players who are just starting to learn openings, the obvious place to start is with the games that you actually play. Naturally, in order to do that, you must keep transcripts of your games, or at least record the openings. Even if you are just playing some informal games, it pays to keep track of your games. Have a computer analyze your games and find your mistakes in the opening. In this manner, you can build up your book one move at a time.

For anyone striving to become a world-class player, it is important to take a more systematic approach to opening research, including studying openings that you have not actually played before. Below I will try to make the process more concrete, but first I want to offer a “big picture” perspective that might help guide you in your opening research.

The perfect game

Speculation on which side would win a perfectly played game of Othello seems to be as old as the game itself. As even number theory was developed in the 1980’s, it seemed that the advantage of the last move gave White a slight edge. Now with the benefit of strong computer programs, it appears that a perfectly played game of Othello would end in a draw. While it will be a long time before computers are powerful enough to prove this conclusively, until someone comes up with a way to win for one side or the other, we might as well accept it as though it was fact.

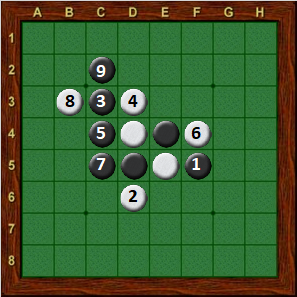
One important conclusion of opening research is that while there are many ways to play for White, Black has very few choices that lead to a draw. For example, Diagrams 11-5 and 11-5 show one opening sequence which appears to lead to a draw. Black could change the order of moves 3 and 5, but other than this there are no choices except for 7. f6, which is also a draw. At move 10, White has three moves that maintain a draw (b4, e3, and e6), and in response to each of these Black again has only one drawing move. In the game shown in Diagram 11-3, Black effectively has no choices, other than move order (e.g., moves 55/56 could be made before moves 53/54 without changing the outcome of the game) throughout the entire game. If Black makes any move other than those shown, White would be winning. Meanwhile, White has choices at several points in the game, including four possible move 22’s.

As White, if you can just memorize the one sequence of moves in Diagram 11-6, you can guarantee that you get a draw (if Black follows the sequence as well), or that you reach a winning position (if Black makes a different move at some point). However, before you sit down to memorize this game, I should point out a couple of problems. First, a draw is not a particularly good result under many circumstances. You could not become World Champion by drawing every game. Second, there is a big difference between having a winning position and actually winning.

Diagram 11-4	Diagram 11-5	Diagram 11-6
	White to move	Perfect game?

While Black has very few ways to maintain a drawing position, there are a huge number of variations which give White a 33-31 win. Even the strongest computer programs can not hold on to every 2-disc advantage early in the game. For humans, even world-class players, 2 discs is not a significant advantage. In fact, in many of these positions, it is more difficult to play white than black; in games between human players of equal strength, Black will win more often than White.

How to decide what openings to put in your book

Given all this, deciding on what book openings to use is not simply a matter of choosing what are theoretically the best moves. Instead, in each particular game, you must choose the moves that will give you the best chance of winning the game. There are many factors to consider: your strengths and weakness, those of your opponent, how many openings you are able to memorize, what openings your opponent knows, the time limit for the game, and so on. Choosing openings is thus more of an art than a science. What works for me probably would not work for you, and what worked in the last game might not work in the next one. There are, however, three general principles that you may find useful.

1. Choose uncommon openings

Since there are no openings that lead to a forced win, and you can not expect to play perfectly, in order to win your opponent must make more mistakes than you do. Thus, we want to maximize the chances of our opponents making a bad move, and often the best way of doing that is to play openings that they have not seen before.

As noted above, in Diagram 11-6, White has four choices at move 22 which lead to a draw. Of these, e8 is by far the most common move— for quite some time, it was believed that this move led to a win for White. Even after it was discovered that e8 was actually draw, it remained the most common move. Naturally, anyone playing this opening with Black would know what to do against this move. Sometime in 1998 I saw several computer games with d1 at move 22 that led to good results for White. After studying it I started playing this move, and won several games in a row with it as my opponents had not seen it before. In theory, e8 is just as good as d1, but at least at that time, d1 was much less common, and much more effective.

2. Choose openings which are easy to learn

Another way to make things difficult for your opponent is to play openings which offer a lot of good choices for your color, but few choices for your opponent. For example, while the sequence in Diagram 11-4 is theoretically the best opening for Black, White has a lot of good choices while Black does not. This means that in order to play this opening well with Black, you must study all of White’s options, whereas your opponent need only study one of the lines. This is a heavy price to pay just to get a theoretical draw.

Compare this to an opening where Black has a slightly inferior position, but Black has a lot of viable options, while in response to each of these options White has only one move which maintains the advantage. In this case, you need only remember a few sequences, while your opponent would have to know many. In my experience, if you prepare such an opening, even world-class players are unable to maintain the advantage for the entire game. Eventually you gain the advantage by knowing the opening to greater depth than your opponents.

3. Do not accept worse than a minus 4 position

As noted above, playing unusual openings is a good way to get your opponent out of his opening book. Sometimes, however, the reason an opening is uncommon is simply that it is bad. In my experience, it is rarely worthwhile to play an opening which computer analysis indicates is worse than minus 4 discs. The problem with such an opening is it usually opens up a lot of reasonable responses by your opponent— even if your opponent makes a mistake, it may still leave you with a losing or at best even position. There are plenty of openings to choose from which are both rarely played and close to even, so there is no need to intentionally play bad moves that leave you with a significant disadvantage. By the same token, when deciding on which of your opponent’s options to prepare for, it usually does not pay to look at positions where you are ahead by more than 4 discs; if you get ahead by that much the opening has done its job.

Trade-off between goals

In general, there is a trade-off between the above-mentioned principles. Since everyone wants openings which are good and easy to learn (principles 2 and 3), most of these openings have been played before and are well known (violating principle 1). Still, there are always new moves to try if you look for them carefully. Sometimes a good opening falls out of favor for a while, at which point people start to forget about it, offering a chance to surprise someone with it.

It is certainly possible to live only by principle 2 and be successful with openings even when they are well known. Some people specialize in certain openings, playing them in every single game for years. Even if you study the opening, they will know it better than you do, and thus have a good chance of beating you. This sort of strategy will naturally lead to long book openings, and a lot of very close positions going into the endgame. It is thus suited to someone who is good at memorizing openings and at counting in the endgame (see Chapter 13).

Someone who hates studying openings but is strong in the midgame would normally focus only on principle 1 and choose to play unusual openings, even if it means taking a slightly inferior position out of the opening. If the opening is so uncommon that you are certain your opponent will not know it, then principle 2 is not important. In such a case, you are not planning to beat your opponent with the opening. Rather, you simply want to force your opponent out of his book and try to win by out-playing him the rest of the game. If you are substantially better than your opponent at the midgame and endgame, taking a position which is inferior by 4 discs is not an unreasonable price to pay.

Looking back at history, I would argue that no one who has taken an extreme approach to openings has ever become World Champion. No matter how strong you are in the rest of the game, if you always play bad openings to force your opponents out of book, it is difficult to come from behind and win a high percentage of games. If you take the other extreme and try to memorize commonly played computer moves until move 60, you end up with a lot of very close games at move 40, and again it is hard to win a high percentage of games. For most players, I suggest a compromise approach: try to get your opponent out of his opening book, but do not resort to taking bad positions in order to do so.

Using WZebra to develop an opening

In light of the above, let us think about developing a practical opening book to use against the chimney (Diagram 11-1) as Black. Again, this is more of an art than a science, and there are many factors which depend on your individual needs, but working through a brief example should give you the basic idea. First, we must decide on what to play at move 7. Table 11-1 shows some of the factors that we might consider.

The column labelled “evaluation” shows how WZebra rates each move at a search depth of 24 moves. We could simply choose the move with the best evaluation, but keep in mind principles 1 and 2. “Frequency” is the percentage of games (in the Thor database) in which each move was chosen. Usually, the lower the percentage, the better the chances are for knocking your opponent out of his opening book. Note that there is some decision involved in which games to include in the analysis. I would argue that any game more than 10 years old is probably irrelevant, and 5 years or even 2 years could be the cutoff.

“Branches better than -2” indicates the number of White’s choices at move 8 that WZebra rates better than -2.00. This gives some indication of how many moves we will have to include if we want to extend our book to move 9. In practice, we would normally want to look further out along the tree to see how many good options each side has. Again, by principle 2, we want a lot of options for Black, and few options for White. Note that -2 as the cutoff is arbitrary; for some openings I might use zero, for others -4 would make more sense.

Table 11-1
Move	Evaluation	Frequency	Branches better than -2	White found decent reply	Branches frequency >10%
c4	-2.38	22%	2	84%	2
c5	-3.75	7%	2	85%	1
c6	-2.16	3%	2	78%	3
e7	-1.94	6%	3	84%	4
g4	-1.08	58%	1	86%	1
g5	-2.98	3%	3	100%	2
g6	-2.41	1%	2	100%	2

Note: This table constructed with WZebra 4.2.1-- your mileage may vary

In that regard, the column “white found decent reply” shows the percentage of games in which white found one of the moves included under the “branches better than -2” column. After all, we are hoping that our opponent is going to make a bad move, so it is good to know how frequently players have made mistakes facing the same position. The column labelled “branches frequency >10%” indicates, following Black’s move 7, the number of White replies at move 8 which were used in more than 10% of the games in the database. Again, this gets at the issue of how many lines we will need to extend our opening book to move 9 or beyond. To be safe, it is best to consider White’s moves if WZebra rates them highly or if they have been used frequently in actual play.

Given all this information, we can start to get some idea of the advantages and disadvantages of each choice at move 7. The move which WZebra rates the highest, g4, is played in a majority of games. There is only one good choice for White at 8, and it is natural to expect that any expert player would know this move. Thus, playing g4 triggers a semiautomatic response at 8, and we need to research the opening from move 9 onward.

By contrast, 7. c6 is given a slightly lower evaluation, but has been played only 3% of the time, which should mean that most players will not have studied it extensively. White has 2 reasonable choices at 8 and you should expect most of your opponents to find one of them, but with a bit more research at move 9 or beyond, you might be able to stay in your opening book longer than your opponent. You must then figure out whether that is likely to translate into getting an advantageous position.

One way to test a move like 7. c6 is to play out a few games against yourself, trying some plausible-looking variations for each side. If you have not tried it before, it can be tricky to play against yourself, but it is a very good way to practice and to develop a feel for an opening. Suppose that you used a computer to study an opening, and reach a position where White is supposed to have a 4 disc advantage after move 20. When you play out the game for both sides, you might find that despite this theoretical advantage, Black ends up winning every time. In this case, you are unlikely to be successful with the opening as White unless you memorize more of the correct moves later in the game.

Conclusion

Although I would like to provide you with a surefire method for getting through the opening with an advantage, it should be clear by now that there is no way to do so. While complicated, the above analysis barely scratches the surface on all of the factors that you could consider when choosing an opening. There is simply no right or wrong answer.

Regardless of the approach you adopt, it is important to spend at least some of your practice time studying openings, especially if you aspire to be an expert player. I strongly urge you to record your games and study the openings. Write down the results of your research in a book, and make cheat sheets so that you can learn openings in a systematic way.

---

Navigation: Main Page > Learn Othello > Book Rose

‎<< previous chapter << - >> next chapter >>